

That is the reason why the formula √ is known as Heron's formula.An isosceles triangle is a triangle that has two sides of equal length. Heron's formula is named after the Heron of Alexandria, a Greek mathematician, who found the area of a triangle using the 3 sides. Heron's formula is written as, Area = √, where a, b and c are the sides of the triangle, and 's' is the semi-perimeter of the triangle. Heron's formula is used to find the area of a triangle that has three different sides. So it is not possible to find the sides of a triangle if we just know all 3 angles, we need to know at least one side to determine the other two sides. Thus, there are an infinite number of triangles with the same set of any three given angles. Let us recall the fact that two similar triangles have the same angles but different sides (sides are in proportion).
#Base of isosceles triangle calculator how to
How to Find the Length of the sides of a Triangle with 3 Angles Only? According to the Heron's formula: Area = √, where, a, b and c are the sides of the triangle, and 's' is the semi-perimeter of the triangle. An irregular triangle means a triangle whose sides are different in length. We use the Heron's formula to find the area of an irregular triangle. How do you find the Area of an Irregular Triangle? It is also known as a scalene triangle (if all three sides are different). Substituting the values in the formula, √ = √(7.5 × 4.5 × 2.5 × 0.5) = 6.49 unit 2 What is an Irregular Triangle?Īn irregular triangle is a triangle in which all three sides are of different lengths. In this case, a = 3, b = 5, c = 7, and s (semi perimeter) = 7.5. If the three sides of a triangle are given as 3, 5 and 7, its area can be calculated with the formula, area = √. What is the Area of a Triangle with Sides 3, 5, 7? For example, if two sides of a triangle are 5 units and 7 units and the included angle is 60°, then, Area = (7 × 5 × sin 60)/2 = 15.15 square units. This is also known as the "side angle side " method. If the sides of a triangle are given along with an included angle, the area of the triangle can be calculated with the formula, Area = (ab × sin C)/2, where 'a' and 'b' are the two given sides and C is the included angle. What is the Area of a Triangle with three Sides and an Angle? For example, if the height (altitude) of a triangle = 8 units, and the side of the triangle on which the altitude is formed is given (base) = 7 units, we can find its area using the formula, Area of a triangle = 1/2 × base × height. Area of a triangle = 1/2 × base × height. If we know the sides of a triangle along with its height, we can use the basic formula for the area of a triangle. What is the Area of Triangle with 3 Sides and Height? For example, if an equilateral triangle has a side of 6 units, its area will be calculated as follows. The area of an equilateral triangle can be calculated using the formula, Area = a 2(√3/4), where 'a' is the side of the triangle.

If a triangle has 3 equal sides, it is called an equilateral triangle. 's' be calculated as follows: semi perimeter = (a + b + c)/2 What is the Area of Triangle with 3 Sides Equal Sides? The area of a triangle with 3 sides can be calculated with the help of the Heron's formula according to which, the area of a triangle is √, where a, b, and c, are the three different sides and 's' is the semi perimeter of the triangle. \( \begin\)įAQs on Area of Triangle with 3 Sides What is the Area of a Triangle With 3 Sides? Using one of the Trigonometric identities, Using law of cosines, cos A = (b 2 + c 2 - a 2) / 2bc. The proof of the formula for the area of triangle with 3 sides can be derived in the following way.Ĭonsider the triangle shown above with sides a, b, c, and the opposite angles to the sides as angle A, angle B, angle C. How to Find Area of Triangle with Three Sides? Proof of Area of Triangle with 3 Sides Formula This formula was derived by a Greek mathematician known as the Heron of Alexandria. However, if the altitude of a triangle is not known, and we need to find the area of triangle with 3 different sides, the Heron's formula is used. The basic formula that is used to find the area of a triangle is ½ × Base × Height where "Base" is the side of the triangle on which the altitude is formed, and "Height" is the length of the altitude drawn to the "Base" from its opposite vertex. The area of a triangle can be calculated with the help of various formulas.
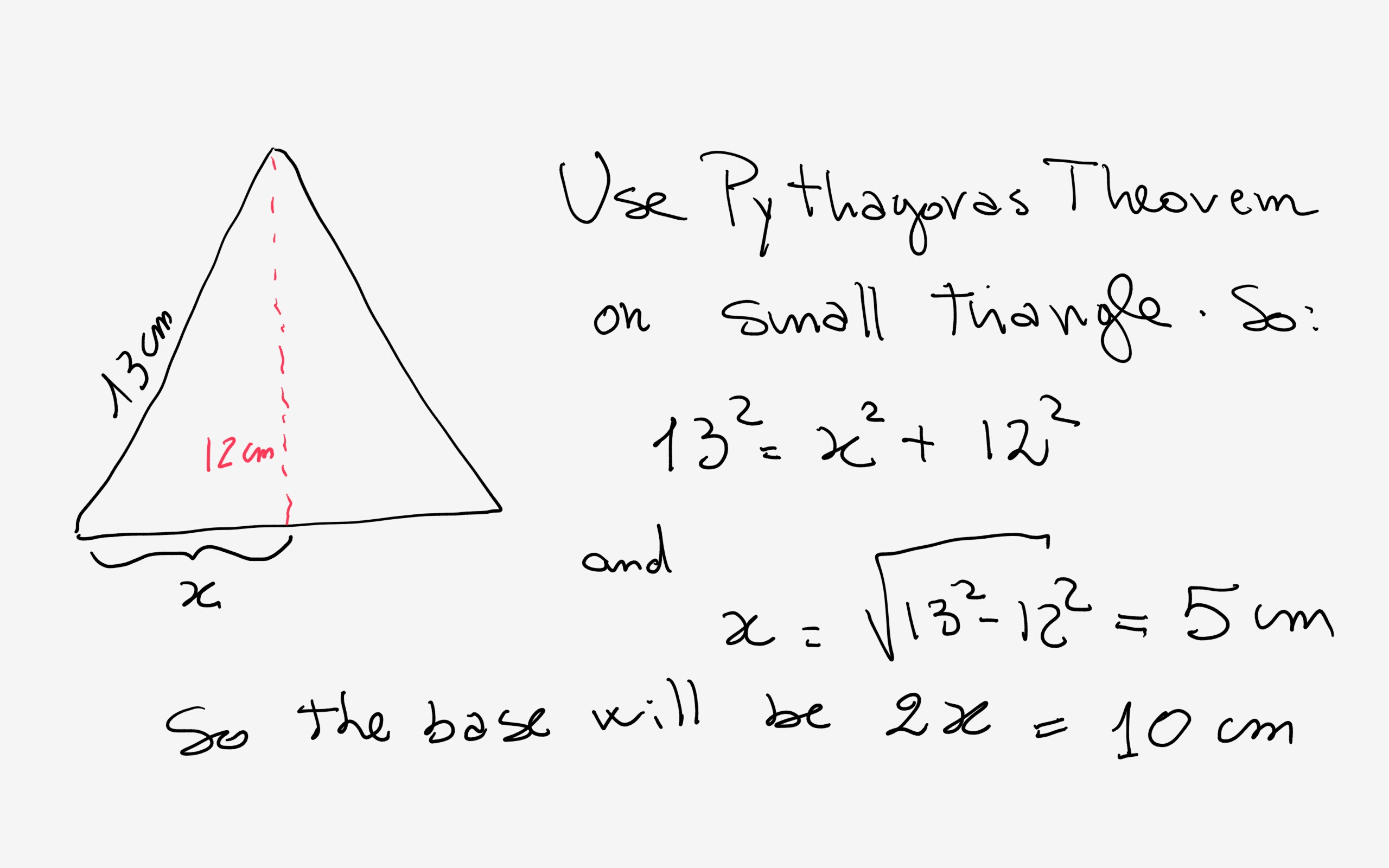
Using this, the area of a triangle (A) with 3 sides a, b, and c is calculated using the formula A = √, where 's' is the semi-perimeter of the triangle given by s = (a + b + c)/2. In order to find the area of triangle with 3 sides, we use the Heron's Formula.


 0 kommentar(er)
0 kommentar(er)
